Semi-Empirical Mathematical Modeling, Energy and Exergy Analysis, and Textural Characteristics of Convectively Dried Plantain Banana Slices
Abstract
:1. Introduction
2. Materials and Methods
2.1. Collection of Raw Material
2.2. Drying Experiment
2.3. Determination of Moisture Content, Moisture Ratio, and Drying Rate
2.4. Fitting of Semi-Empirical Mathematical Models
2.5. Determination of Effective Moisture Diffusivity
2.6. Determination of Activation Energy
2.7. Mass Transfer Properties
2.8. Process Energy Consumption
2.9. Texture Analysis
2.10. Statistical Analysis
3. Results and Discussion
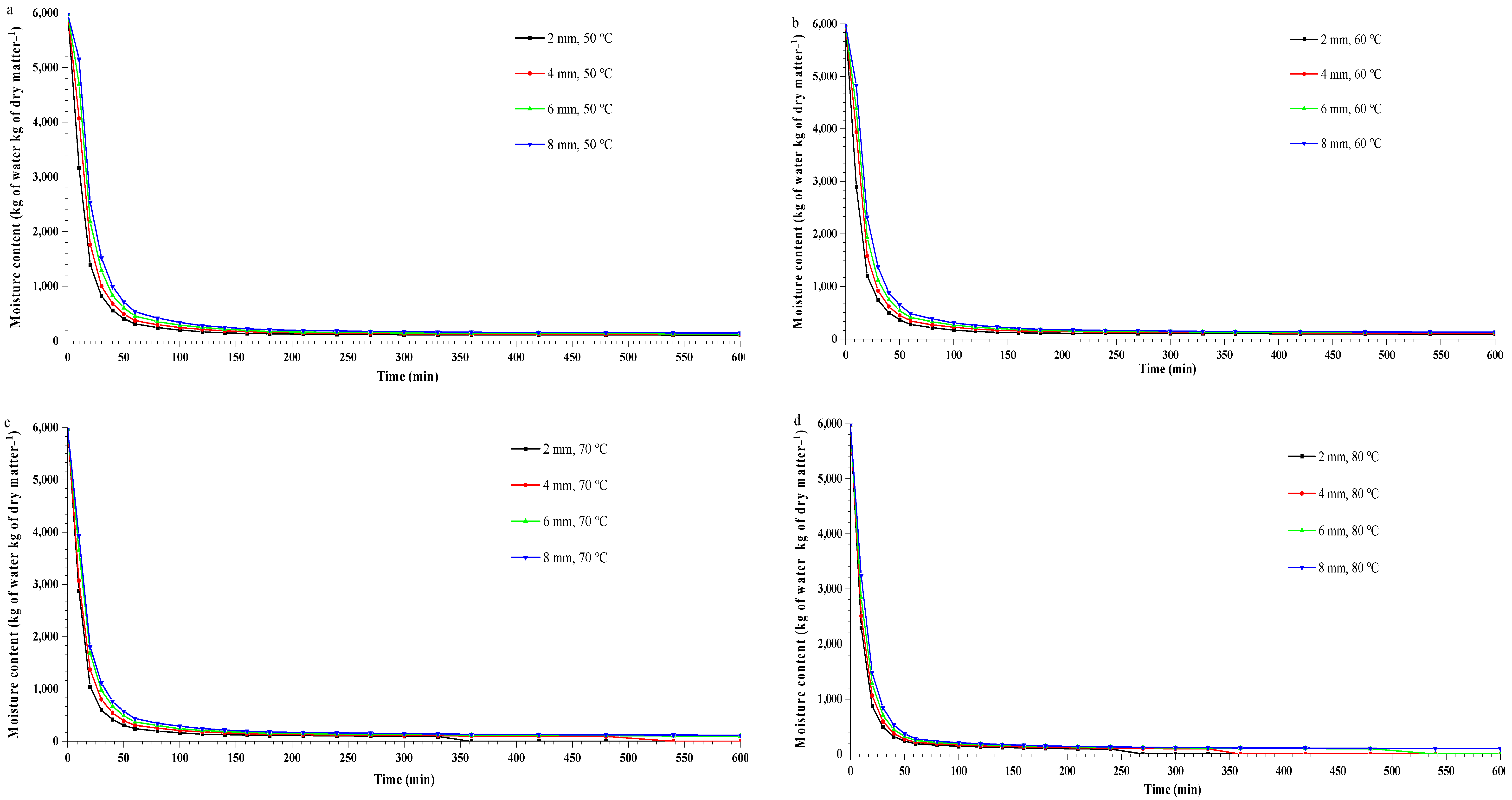
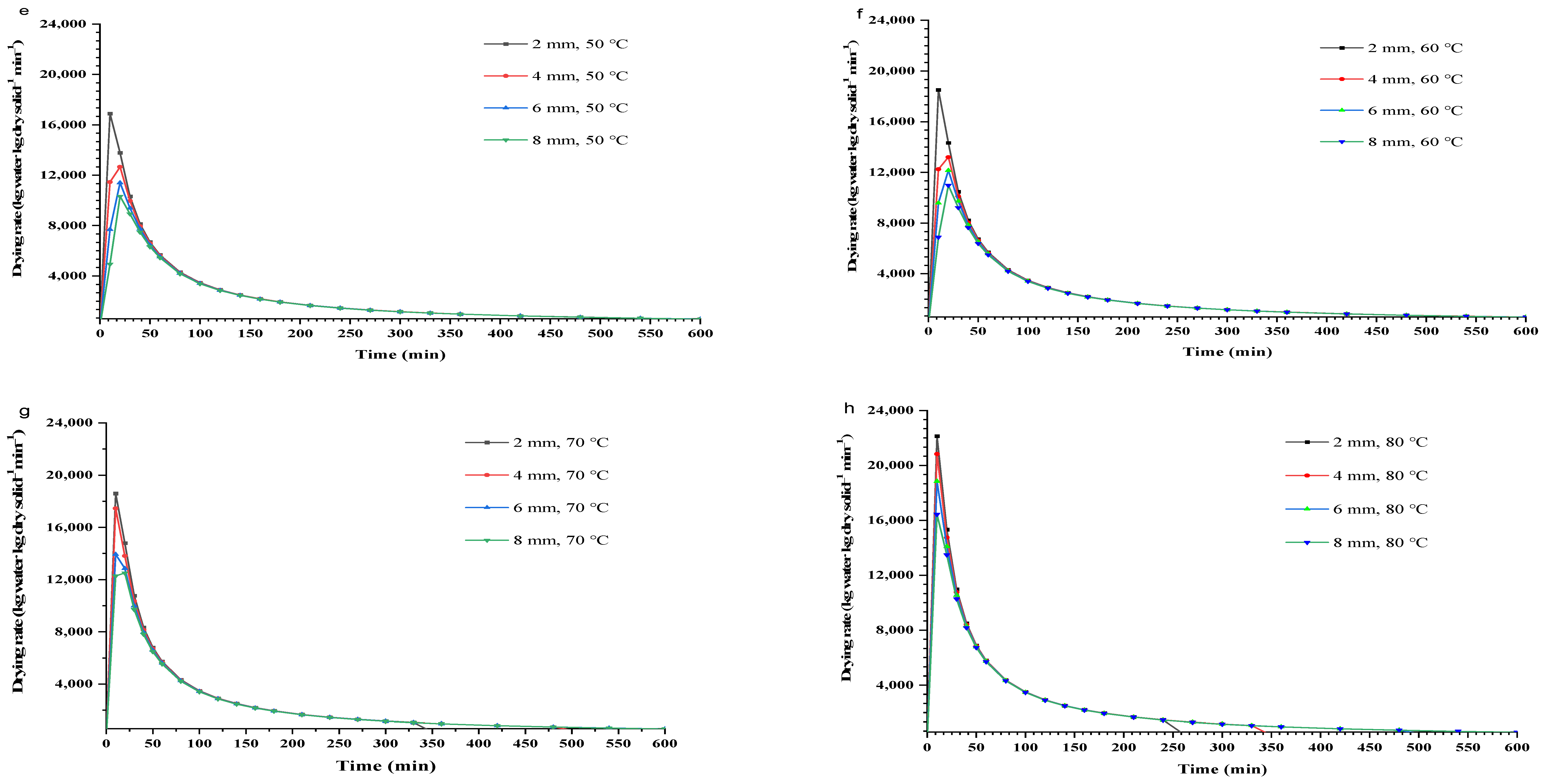
3.1. Drying Characteristics
3.2. Model Fitting on Drying Curve
3.3. Effective Moisture Diffusivity
3.4. Activation Energy
3.5. Mass Transfer Properties
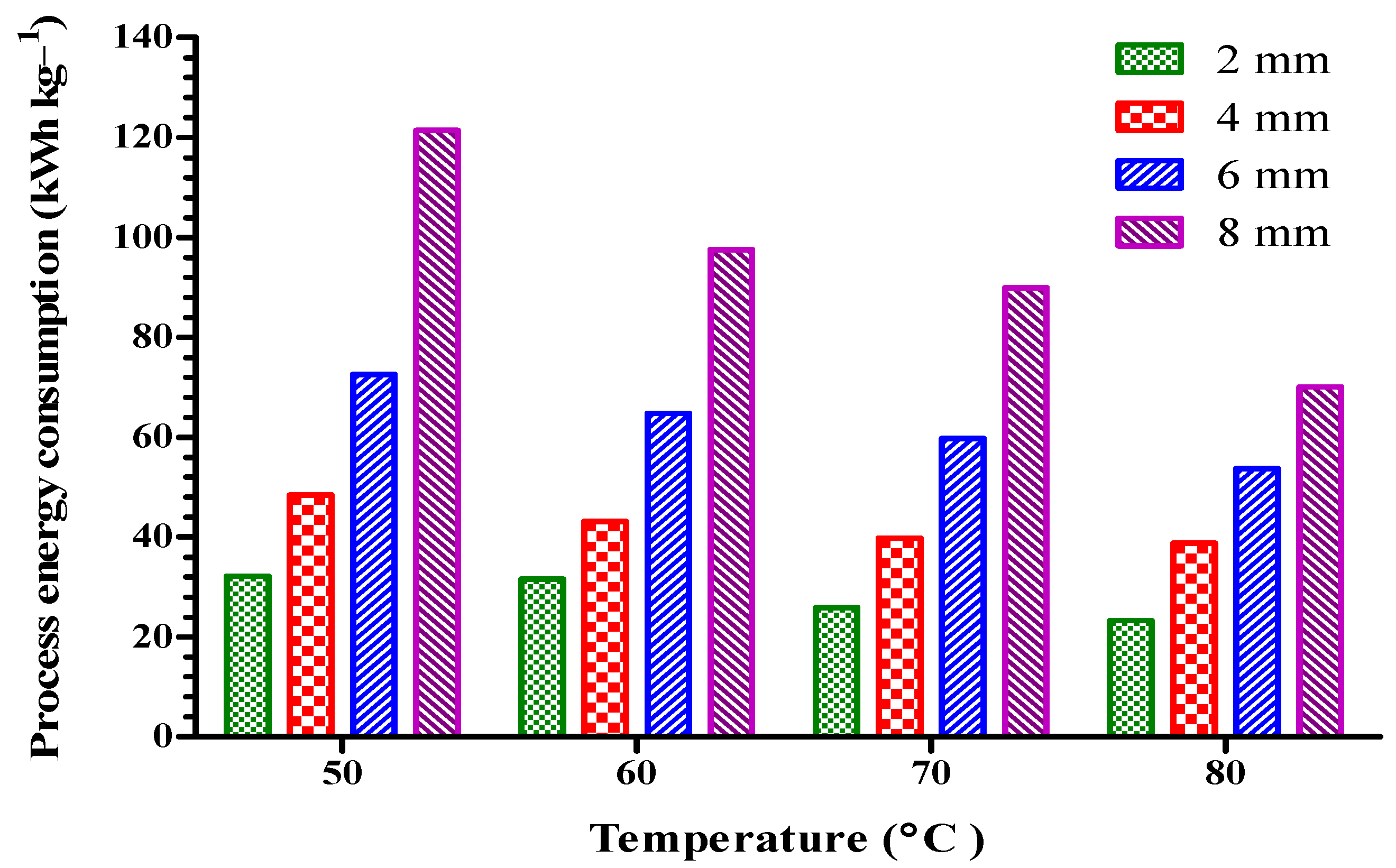
3.6. Process Energy Consumption
3.7. Texture
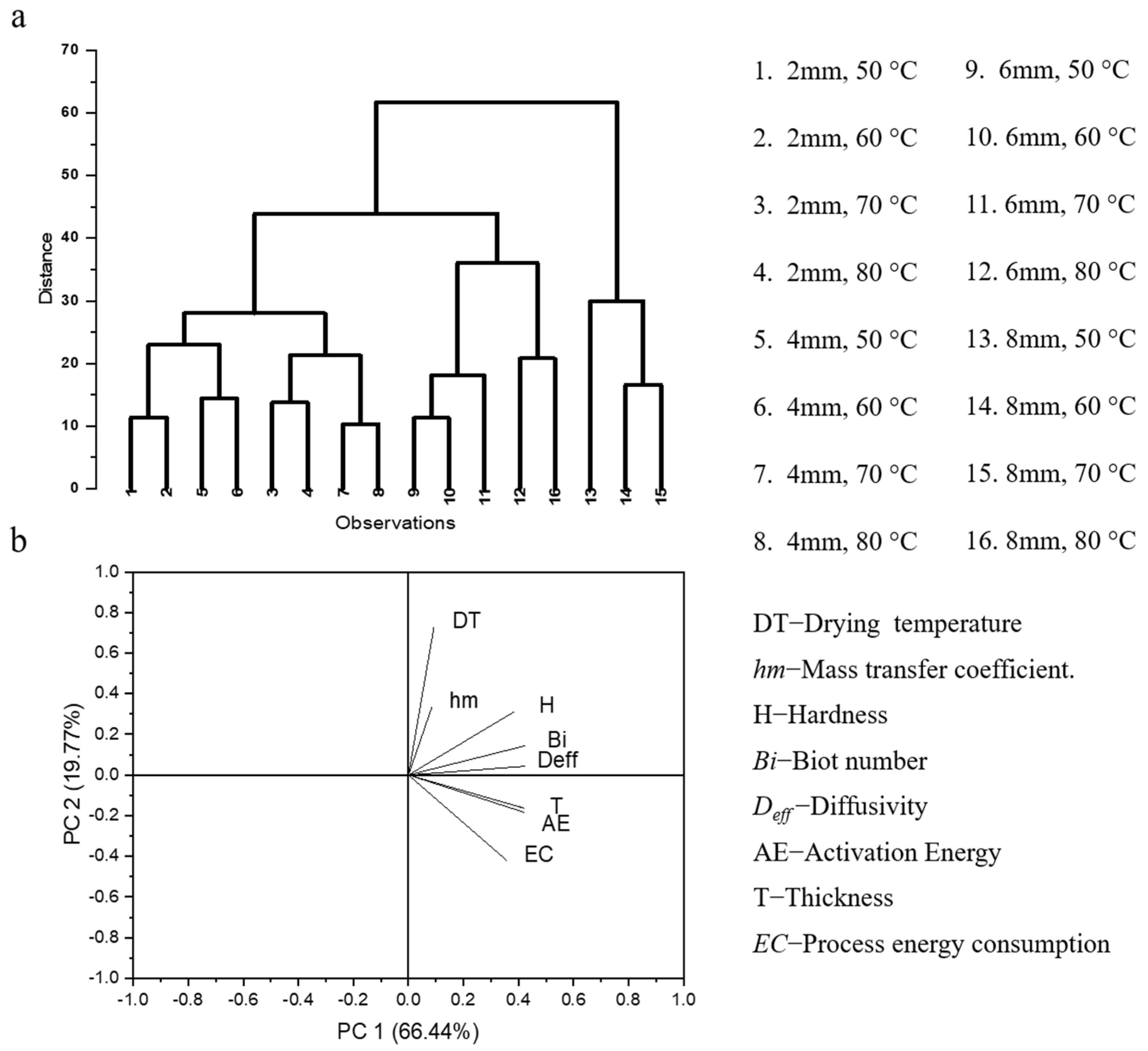
3.8. Compound Correlation Study
4. Conclusions
5. Practical Applications
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- India Exports Bananas Worth Rs 619 cr during 2020–2021—The Economic Times. Available online: https://economictimes.indiatimes.com/news/economy/foreign-trade/india-exports-bananas-worth-rs-619-cr-during-2020-21/articleshow/83566756.cms (accessed on 22 February 2022).
- Food and Agriculture Organization of the United Nations, Rome. Available online: http://www.fao.org/faostat/en/#data/QC/visualize (accessed on 22 February 2022).
- Odenigbo, M.A.; Asumugha, V.U.; Ubbor, S.; Nwauzor, C.; Otuonye, A.C.; Offia-Olua, B.I.; Princewill-Ogbonna, I.L.; Nzeagwu, O.C.; Henry-Uneze, H.N.; Anyika, J.U.; et al. Proximate composition and consumption pattern of plantain and cooking-banana. Br. J. Appl. Sci. 2013, 3, 1035–1043. [Google Scholar] [CrossRef]
- Falcomer, A.L.; Riquette, R.F.; de Lima, B.R.; Ginani, V.C.; Zandonadi, R.P. Health benefits of green banana consumption: A systematic review. Nutrients 2019, 11, 1222. [Google Scholar] [CrossRef] [PubMed]
- Ojediran, J.O. Thin layer drying of millet and effect of temperature on drying characteristics. Int. Food Res. J. 2010, 17, 1095–1106. [Google Scholar]
- Doymaz, İ. Thin-layer drying characteristics of sweet potato slices and mathematical modelling. Heat Mass Transf. 2011, 47, 277–285. [Google Scholar] [CrossRef]
- Omari, A.; Behroozi-Khazaei, N.; Sharifian, F. Drying kinetic and artificial neural network modeling of mushroom drying process in microwave-hot air dryer. J. Food Process Eng. 2018, 41, 12849–12859. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Price, W.E. Air-drying of banana: Influence of experimental parameters, slab thickness, banana maturity and harvesting season. J. Food Eng. 2007, 79, 200–207. [Google Scholar] [CrossRef]
- Pico, J.; Xu, K.; Guo, M.; Mohamedshah, Z.; Ferruzzi, M.G.; Martinez, M.M. Manufacturing the ultimate green banana flour: Impact of drying and extrusion on phenolic profile and starch bioaccessibility. Food Chem. 2019, 297, 124990–125000. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Janius, R.B.; Nawi, N.M.; Abdan, K. Modeling the thin-layer drying of fruits and vegetables: A review. Compr. Rev. Food Sci. Food Saf. 2016, 15, 599–618. [Google Scholar] [CrossRef]
- Beigi, M. Energy efficiency and moisture diffusivity of apple slices during convective drying. Food Sci. Technol. 2016, 36, 145–150. [Google Scholar] [CrossRef]
- Takougnadi, E.; Boroze, T.E.; Azouma, O.Y. Development of an intermittent drying process of onion. Cogent Food Agric. 2018, 4, 1422225. [Google Scholar] [CrossRef]
- Torki-Harchegani, M.; Ghanbarian, D.; Sadeghi, M. Estimation of whole lemon mass transfer parameters during hot air drying using different modelling methods. Heat Mass Transf. 2015, 51, 1121–1129. [Google Scholar] [CrossRef]
- John, S.G.; Sangamithra, A.; Veerapandian, C.; Sasikala, S.; Sanju, V. Mathematical modelling of the thin layer drying of banana blossoms. J. Nutr. Health Food Eng. 2014, 1, 42–49. [Google Scholar] [CrossRef]
- Kabiru, A.A.; Joshua, A.A.; Raji, A.O. Effect of slice thickness and temperature on the drying kinetics of mango (Mangifera indica). Int. J. Res. Rev. Appl. Sci. 2013, 15, 41–50. [Google Scholar]
- Olurin, T.O.; Adelekan, A.O.; Olosunde, W.A. Mathematical modelling of drying characteristics of blanched field pumpkin (Cucurbita pepo L.) slices. Agric. Eng. Int. CIGR J. 2012, 14, 246–254. [Google Scholar]
- Rayaguru, K.; Routray, W. Mathematical modeling of thin layer drying kinetics of stone apple slices. Int. Food Res. J. 2012, 19, 1503–1510. [Google Scholar]
- Kaleta, A.; Górnicki, K. Evaluation of drying models of apple (var. McIntosh) dried in a convective dryer. Int. J. Food Sci. Technol. 2010, 45, 891–898. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Bicer, Y.; Yildiz, C. Thin layer drying of red pepper. J. Food Eng. 2003, 59, 99–104. [Google Scholar] [CrossRef]
- Yaldýz, O.; Ertekýn, C. Thin layer solar drying of some vegetables. Dry. Technol. 2001, 19, 583–597. [Google Scholar] [CrossRef]
- Sun, S.H.; Kim, S.J.; Kwak, S.J.; Yoon, K.S. Efficacy of sodium hypochlorite and acidified sodium chlorite in preventing browning and microbial growth on fresh-cut produce. Prev. Nutr. Food Sci. 2012, 17, 210–216. [Google Scholar] [CrossRef]
- AOAC. Official Methods of Analysis; AOAC: Washington, DC, USA, 2003. [Google Scholar]
- Kumar, P.S.; Nambi, E.; Shiva, K.N.; Vaganan, M.M.; Ravi, I.; Jeyabaskaran, K.J.; Uma, S. Thin layer drying kinetics of Banana var. Monthan (ABB): Influence of convective drying on nutritional quality, microstructure, thermal properties, color, and sensory characteristics. J. Food Process Eng. 2019, 42, e13020. [Google Scholar] [CrossRef]
- Song, X.D.; Mujumdar, A.S.; Law, C.L.; Fang, X.M.; Peng, W.J.; Deng, L.Z.; Wang, J.; Xiao, H.W. Effect of drying air temperature on drying kinetics, color, carotenoid content, antioxidant capacity and oxidation of fat for lotus pollen. Dry. Technol. 2020, 38, 1151–1164. [Google Scholar] [CrossRef]
- Singh, A.; Sarkar, J.; Sahoo, R.R. Experimental energy-exergy performance and kinetics analyses of compact dual-mode heat pump drying of food chips. J. Food Process Eng. 2020, 43, e13404. [Google Scholar] [CrossRef]
- Guiné, R.P.; Barroca, M.J.; Silva, V. Mass transfer properties of pears for different drying methods. Int. J. Food Prop. 2013, 16, 251–262. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Dincer, I. Application of moisture transfer models to solids drying. Proc. Inst. Mech. Eng. Part A J. Power Energy 2005, 219, 235–244. [Google Scholar] [CrossRef]
- Guiné, R.P.; Henrriques, F.; Barroca, M.J. Mass transfer coefficients for the drying of pumpkin (Cucurbita moschata) and dried product quality. Food Bioprocess Technol. 2012, 5, 176–183. [Google Scholar] [CrossRef]
- Motevali, A.; Minaei, S.; Khoshtagaza, M.H. Evaluation of energy consumption in different drying methods. Energy Convers. Manag. 2011, 52, 1192–1199. [Google Scholar] [CrossRef]
- Mao, Y.; Flores, R.A.; Loughin, T.M. Objective texture measurements of commercial wheat flour tortillas. Cereal Chem. 2002, 79, 648–653. [Google Scholar] [CrossRef]
- Sharabiani, V.R.; Kaveh, M.; Abdi, R.; Szymanek, M.; Tanaś, W. Estimation of moisture ratio for apple drying by convective and microwave methods using artificial neural network modeling. Sci. Rep. 2021, 11, 9155. [Google Scholar] [CrossRef]
- Srikanth, K.S.; Sharanagat, V.S.; Kumar, Y.; Bhadra, R.; Singh, L.; Nema, P.K.; Kumar, V. Convective drying and quality attributes of elephant foot yam (Amorphophallus paeoniifolius). LWT-Food Sci. Technol. 2019, 99, 8–16. [Google Scholar] [CrossRef]
- Jabeen, R.; Aijaz, T.; Gul, K. Drying kinetics of potato using a self-designed cabinet dryer. Cogent Food Agric. 2015, 1, 1036485. [Google Scholar] [CrossRef]
- Workneh, T.S.; Oke, M.O. The influence of the combined microwave power and hot air ventilation on the drying kinetics and colour quality of tomato slices. Afr. J. Biotechnol. 2012, 11, 15353–15364. [Google Scholar]
- Ojediran, J.O.; Okonkwo, C.E.; Adeyi, A.J.; Adeyi, O.; Olaniran, A.F.; George, N.E.; Olayanju, A.T. Drying characteristics of yam slices (Dioscorea rotundata) in a convective hot air dryer: Application of ANFIS in the prediction of drying kinetics. Heliyon 2020, 6, e03555. [Google Scholar] [CrossRef]
- Taskin, O.; Polat, A.; Etemoglu, A.B.; Izli, N. Energy and exergy analysis, drying kinetics, modeling, microstructure and thermal properties of convective-dried banana slices. J. Therm. Anal. Calorim. 2021, 147, 2343–2351. [Google Scholar] [CrossRef]
- Nachaisin, M.; Jamradloedluk, J.; Niamnuy, C. Application of combined far-infrared radiation and air convection for drying of instant germinated brown rice. J. Food Process Eng. 2016, 39, 306–318. [Google Scholar] [CrossRef]
- Zogzas, N.P.; Maroulis, Z.B.; Marinos-Kouris, D. Moisture diffusivity data compilation in foodstuffs. Dry. Technol. 1996, 14, 2225–2253. [Google Scholar] [CrossRef]
- Falade, K.O.; Olurin, T.O.; Ike, E.A.; Aworh, O.C. Effect of pretreatment and temperature on air-drying of Dioscorea alata and Dioscorea rotundata slices. J. Food Eng. 2007, 80, 1002–1010. [Google Scholar] [CrossRef]
- Ye, L.; EL-Mesery, H.S.; Ashfaq, M.M.; Shi, Y.; Zicheng, H.; Alshaer, W.G. Analysis of energy and specific energy requirements in various drying process of mint leaves. Case Stud. Therm. Eng. 2021, 26, 101113. [Google Scholar] [CrossRef]
- Darvishi, H.; Khodaie, J.; Azadbakht, M. The parameters of mass transfer of convective drying in sliced melon. Philipp. Agric. Sci. 2015, 98, 60–72. [Google Scholar]
- Barragán-Iglesias, J.; Rodríguez-Ramírez, J.; Sablani, S.S.; Méndez-Lagunas, L.L. Texture analysis of dried papaya (Carica papaya L., Cv. Maradol) pretreated with calcium and osmotic dehydration. Dry. Technol. 2019, 37, 906–919. [Google Scholar] [CrossRef]
- Jamradloedluk, J.; Nathakaranakule, A.; Soponronnarit, S.; Prachayawarakorn, S. Influences of drying medium and temperature on drying kinetics and quality attributes of durian chip. J. Food Eng. 2007, 78, 198–205. [Google Scholar] [CrossRef]
- Macedo, L.L.; da Silva Araújo, C.; Vimercati, W.C.; Saraiva, S.H.; Teixeira, L.J. Influence of yacon syrup concentration and drying air temperature on properties of osmotically pre-dehydrated dried banana. Heat Mass Transf. 2021, 57, 441–451. [Google Scholar] [CrossRef]



| Sr. No. | Model Name | Model Equation |
|---|---|---|
| 1 | Modified Page | |
| 2 | Verma | |
| 3 | Page | |
| 4 | Newton/Lewis | |
| 5 | Logarithmic | |
| 6 | Henderson and Pabis | |
| 7 | Diffusion approach |
| Model | Temperature (°C) | Thickness (mm) | Model Parameters | Statistical Parameters | ||
|---|---|---|---|---|---|---|
| R2 | Reduced χ2 | RMSE | ||||
| Diffusion approach model | 50 | 2 | a = 0.88; k = 0.03; b = 0.01 | 0.99 | ||
| 4 | a = 0.86; k = 0.0287; b = 0.0163 | 0.99 | ||||
| 6 | a = 0.85; k = 0.0249; b = 0.0174 | 0.99 | ||||
| 8 | a = 0.83; k = 0.0226; b = 0.0186 | 0.99 | ||||
| 60 | 2 | a = 0.88; k = 0.0347; b = 0.0142 | 0.99 | |||
| 4 | a = 0.86; k = 0.0304; b = 0.0177 | 0.99 | ||||
| 6 | a = 0.85; k = 0.0269; b = 0.0182 | 0.99 | ||||
| 8 | a = 0.84; k = 0.0238; b = 0.0177 | 0.99 | ||||
| 70 | 2 | a = 0.87; k = 0.0402; b = 0.0329 | 0.99 | |||
| 4 | a = 0.84; k = 0.0351; b = 0.0411 | 0.99 | ||||
| 6 | a = 0.84; k = 0.0302; b = 0.0343 | 0.99 | ||||
| 8 | a = 0.83; k = 0.0278; b = 0.0284 | 0.99 | ||||
| 80 | 2 | a = 0.88; k = 0.0465; b = 0.0292 | 0.99 | |||
| 4 | a = 0.86; k = 0.0427; b = 0.0323 | 0.99 | ||||
| 6 | a = 0.85; k = 0.0386; b = 0.0291 | 0.99 | ||||
| 8 | a = 0.86; k = 0.0341; b = 0.0233 | 0.99 | ||||
| Sr. No. | Thickness (mm) | Drying Temperature (°C) | Hardness (N) | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 50 | 0.57 | 13.70 | 15.25 ± 3.20 ax | ||
| 2 | 60 | 0.59 | 17.54 ± 5.21 ax | ||||
| 3 | 70 | 0.62 | 23.75 ± 6.58 ax | ||||
| 4 | 80 | 0.66 | 31.84 ± 2.02 ay | ||||
| 5 | 4 | 50 | 0.71 | 15.82 | 26.56 ± 11.74 abx | ||
| 6 | 60 | 0.73 | 35.70 ± 9.40 bx | ||||
| 7 | 70 | 0.77 | 37.02 ± 9.57 bx | ||||
| 8 | 80 | 0.82 | 38.67 ± 6.48 ax | ||||
| 9 | 6 | 50 | 0.78 | 16.93 | 38.23 ± 4.06 bx | ||
| 10 | 60 | 0.81 | 39.95 ± 5.71 bx | ||||
| 11 | 70 | 0.84 | 45.76 ± 4.76 bcx | ||||
| 12 | 80 | 0.92 | 66.13 ± 9.57 by | ||||
| 13 | 8 | 50 | 0.84 | 18.23 | 39.8 ± 5.26 bcx | ||
| 14 | 60 | 0.86 | 41.65 ± 7.30 bx | ||||
| 15 | 70 | 0.91 | 50.36 ± 6.58 cx | ||||
| 16 | 80 | 0.98 | 71.41 ± 2.25 by |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamble, M.G.; Singh, A.; Kumar, N.; Dhenge, R.V.; Rinaldi, M.; Chinchkar, A.V. Semi-Empirical Mathematical Modeling, Energy and Exergy Analysis, and Textural Characteristics of Convectively Dried Plantain Banana Slices. Foods 2022, 11, 2825. https://doi.org/10.3390/foods11182825
Kamble MG, Singh A, Kumar N, Dhenge RV, Rinaldi M, Chinchkar AV. Semi-Empirical Mathematical Modeling, Energy and Exergy Analysis, and Textural Characteristics of Convectively Dried Plantain Banana Slices. Foods. 2022; 11(18):2825. https://doi.org/10.3390/foods11182825
Chicago/Turabian StyleKamble, Meenatai G., Anurag Singh, Navneet Kumar, Rohini V. Dhenge, Massimiliano Rinaldi, and Ajay V. Chinchkar. 2022. "Semi-Empirical Mathematical Modeling, Energy and Exergy Analysis, and Textural Characteristics of Convectively Dried Plantain Banana Slices" Foods 11, no. 18: 2825. https://doi.org/10.3390/foods11182825






